تئوری آشوب: اصول، نظریه پردازان و کاربردها
تئوری آشوب یکی از مفاهیم پیچیده و جذاب در علم ریاضی و فیزیک است که به بررسی سیستمهای دینامیکی غیرخطی و رفتارهای پیچیده و غیرقابل پیشبینی آنها میپردازد. این نظریه که در دهههای اخیر بهطور گستردهای توسعه یافته، نه تنها در علوم طبیعی بلکه در علوم اجتماعی، اقتصادی و مدیریتی نیز کاربردهای فراوانی پیدا کرده است. در این مقاله، به بررسی اصول این حوزه، نظریه پردازان مهم این حوزه و کاربردهای آن خواهیم پرداخت.
اصول تئوری آشوب
تئوری آشوب به مطالعه سیستمهای دینامیکی میپردازد که رفتار آنها به شدت به شرایط اولیه وابسته است، به گونهای که تغییرات کوچک در این شرایط میتواند منجر به تغییرات بزرگ و غیرقابل پیشبینی در آینده شود. برخی از اصول کلیدی این نظریه عبارتند از:
- حساسیت به شرایط اولیه: یکی از مهمترین ویژگیهای سیستمهای آشوبی، حساسیت شدید به شرایط اولیه است. این بدان معناست که تغییرات کوچک در ورودیها میتواند نتایج بسیار متفاوتی به دنبال داشته باشد.
- ساختار فراکتالی: بسیاری از سیستمهای آشوبی دارای ساختارهای فراکتالی هستند. فراکتالها، ساختارهایی هستند که در مقیاسهای مختلف تکرار میشوند و به نظر میرسد الگوهای مشابهی در اندازههای متفاوت دارند.
- پیشبینیناپذیری بلندمدت: به دلیل حساسیت به شرایط اولیه، پیشبینی دقیق رفتار سیستمهای آشوبی در بلندمدت غیرممکن است. این سیستمها در کوتاهمدت قابل پیشبینی هستند، اما با گذر زمان، خطاهای پیشبینی به شدت افزایش مییابند.
- رفتار غیرخطی: سیستمهای آشوبی معمولاً رفتارهای غیرخطی از خود نشان میدهند، به این معنا که خروجیها به صورت مستقیم با ورودیها تناسب ندارند و روابط پیچیدهای بین آنها وجود دارد.
نظریه پردازان تئوری آشوب
تئوری آشوب توسط تعدادی از دانشمندان برجسته توسعه یافته است که برخی از مهمترین آنها عبارتند از:
- ادوارد لورنز (Edward Lorenz): لورنز یکی از پیشگامان تئوری آشوب است که در دهه 1960 با مطالعه بر روی مدلهای هواشناسی، مفهوم حساسیت به شرایط اولیه را معرفی کرد. او نشان داد که حتی تغییرات جزئی در دادههای ورودی مدلهای هواشناسی میتواند منجر به تفاوتهای عمدهای در پیشبینیها شود.
- بنوآ مندلبرات (Benoît Mandelbrot): مندلبرات به خاطر کارهایش در زمینه فراکتالها مشهور است. او نشان داد که بسیاری از پدیدههای طبیعی دارای ساختارهای فراکتالی هستند و این ساختارها را میتوان با استفاده از ریاضیات توصیف کرد.
- میچل فایگنباوم (Mitchell Feigenbaum): فایگنباوم به خاطر کشف روابط ریاضی خاص در سیستمهای آشوبی شناخته شده است. او ثابت کرد که رفتارهای آشوبی در سیستمهای مختلف میتواند با استفاده از ثوابت جهانی توصیف شود.
کاربردهای تئوری آشوب
تئوری آشوب کاربردهای گستردهای در رشتههای مختلف دارد که برخی از مهمترین آنها عبارتند از:
- هواشناسی: همانطور که لورنز نشان داد، تئوری آشوب میتواند توضیح دهد که چرا پیشبینی دقیق وضعیت هوا در بلندمدت غیرممکن است. مدلهای هواشناسی امروزی از مفاهیم تئوری آشوب برای بهبود دقت پیشبینیها استفاده میکنند.
- اقتصاد: بازارهای مالی و اقتصاد کلان نیز میتوانند رفتارهای آشوبی از خود نشان دهند. تحلیلگران مالی از مدلهای آشوبی برای درک بهتر نوسانات بازار و پیشبینی بحرانهای اقتصادی استفاده میکنند.
- زیستشناسی: در زیستشناسی، تئوری آشوب میتواند توضیح دهد که چگونه رفتارهای پیچیده در سیستمهای زیستی مانند جمعیتها و اکوسیستمها شکل میگیرد. مطالعات در این زمینه به بهبود مدیریت منابع طبیعی و حفظ تنوع زیستی کمک میکند.
- فیزیک: بسیاری از پدیدههای فیزیکی، از جریانهای توربولانسی گرفته تا رفتارهای پلاسما، میتوانند با استفاده از تئوری آشوب توصیف شوند. این نظریه به فیزیکدانان کمک میکند تا رفتارهای پیچیده و غیرخطی سیستمهای فیزیکی را بهتر درک کنند.
- مدیریت و سازماندهی: در مدیریت و سازماندهی، تئوری آشوب میتواند به مدیران کمک کند تا با عدم قطعیتها و پیچیدگیهای محیط کسبوکار بهتر مقابله کنند. این نظریه ابزارهای جدیدی برای برنامهریزی استراتژیک و مدیریت تغییر ارائه میدهد.
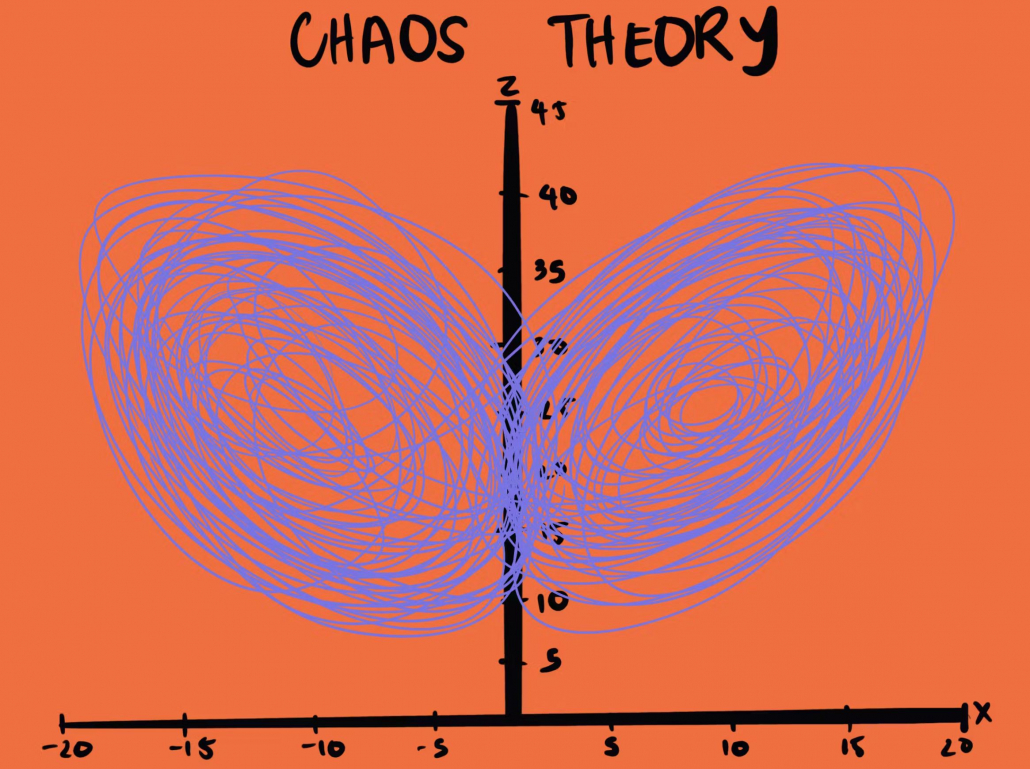
اثر پروانه ای در تئوری آشوب
اثر پروانهای (Butterfly Effect) یکی از مفاهیم جذاب و پیچیده در نظریه آشوب است که به بررسی چگونگی تأثیر تغییرات کوچک در سیستمهای پویا میپردازد. این مفهوم نه تنها در علوم طبیعی بلکه در مدیریت و کسب و کار نیز کاربردهای فراوانی دارد.
نتیجهگیری
تئوری آشوب یکی از مهمترین و پیچیدهترین مفاهیم علمی است که به درک بهتر رفتارهای پیچیده و غیرقابل پیشبینی سیستمهای دینامیکی کمک میکند. اصول کلیدی این نظریه شامل حساسیت به شرایط اولیه، ساختارهای فراکتالی، پیشبینیناپذیری بلندمدت و رفتارهای غیرخطی است. با توجه به کاربردهای گسترده این موضوع در رشتههای مختلف، از هواشناسی و اقتصاد گرفته تا زیستشناسی و مدیریت، این نظریه به یکی از ابزارهای اساسی برای مطالعه و مدیریت پیچیدگیها و عدم قطعیتها در دنیای امروز تبدیل شده است.
جهت دریافت زمان مشاوره با مشاوران شرکت توسعه کسب و کار راه ایده آل با ما در تماس باشید.



